Taupunkt: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
zurück zu [[Messgrößen|Messgrößen]] | zurück zu [[Messgrößen|Messgrößen]] | ||
<br> | <br> | ||
| Zeile 13: | Zeile 12: | ||
== Definition == | == Definition == | ||
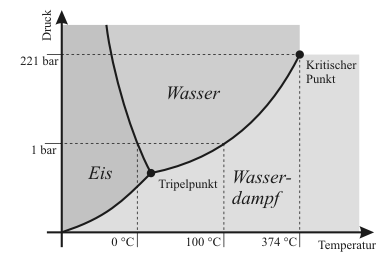
[[Datei:Phasendiagramm | [[Datei:Phasendiagramm Wasser.png|right|thumb|320px|Phasendiagramm des Wassers]] | ||
Der ''Taupunkt'' von Wasser im formalen Sinne ist der Kondensationspunkt reinen Wassers und damit ein Wertepaar aus Druck und Temperatur. Da sich diese jedoch an der Phasengrenzlinie eines Reinstoffes gegenseitig bedingen, hier im Speziellen der Kondensationskurve zwischen Tripelpunkt und kritischem Punkt, setzt man in der Regel den Temperaturwert des Taupunkts, also die '''Taupunkttemperatur''', mit dem Taupunkt gleich. Es handelt sich dabei um diejenige Temperatur der feuchten Luft, bei der diese wasserdampfgesättigt wäre sowie bei abnehmender Temperatur kondensieren würde. In diesem Zustand würde die [[Luftfeuchtigkeit#Relative Luftfeuchtigkeit|relative Luftfeuchte]] 100 % betragen und es herrschte der Sättigungsdampfdruck. Demnach hat diese bzw. dieser auch das Formelzeichen ''T''<sub>d</sub> bei Angaben in K und ''t''<sub>d</sub> oder <math>\vartheta_{\rm d}</math> bei Angaben in °C, wobei der Index ''d'' für das englische „dew point“ steht. Zusätzlich wird auch ''τ'' häufig als Formelzeichen gebraucht. | Der ''Taupunkt'' von Wasser im formalen Sinne ist der Kondensationspunkt reinen Wassers und damit ein Wertepaar aus Druck und Temperatur. Da sich diese jedoch an der Phasengrenzlinie eines Reinstoffes gegenseitig bedingen, hier im Speziellen der Kondensationskurve zwischen Tripelpunkt und kritischem Punkt, setzt man in der Regel den Temperaturwert des Taupunkts, also die '''Taupunkttemperatur''', mit dem Taupunkt gleich. Es handelt sich dabei um diejenige Temperatur der feuchten Luft, bei der diese wasserdampfgesättigt wäre sowie bei abnehmender Temperatur kondensieren würde. In diesem Zustand würde die [[Luftfeuchtigkeit#Relative Luftfeuchtigkeit|relative Luftfeuchte]] 100 % betragen und es herrschte der Sättigungsdampfdruck. Demnach hat diese bzw. dieser auch das Formelzeichen ''T''<sub>d</sub> bei Angaben in K und ''t''<sub>d</sub> oder <math>\vartheta_{\rm d}</math> bei Angaben in °C, wobei der Index ''d'' für das englische „dew point“ steht. Zusätzlich wird auch ''τ'' häufig als Formelzeichen gebraucht. | ||
== Bedeutung für die Meteorologie == | == Bedeutung für die Meteorologie == | ||
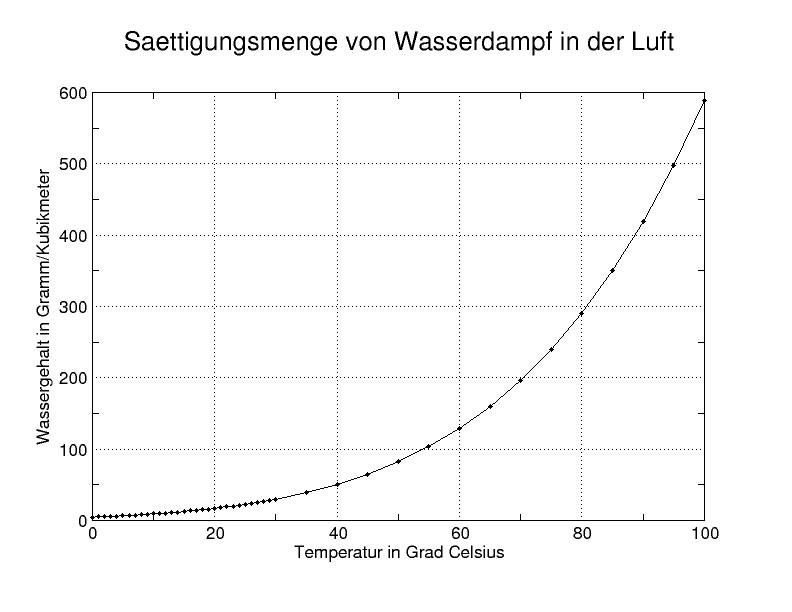
[[Datei:Feuchte Luft.png|thumb|Maximale Wasserdampfkonzentration in Abhängigkeit von der Temperatur]] | [[Datei:Feuchte Luft.png|thumb|310px|Maximale Wasserdampfkonzentration in Abhängigkeit von der Temperatur]] | ||
In der Meteorologie gibt der Taupunkt die Grenztemperatur an, bei der, in Abhängigkeit vom Luftdruck, der in der Luft enthaltene Wasserdampf gerade damit beginnt Kondensat (Tropfen, Eiskristalle) zu bilden. | In der Meteorologie gibt der Taupunkt die Grenztemperatur an, bei der, in Abhängigkeit vom Luftdruck, der in der Luft enthaltene Wasserdampf gerade damit beginnt Kondensat (Tropfen, Eiskristalle) zu bilden. | ||
| Zeile 44: | Zeile 43: | ||
== Berechnung von Taupunkt und Frostpunkt == | == Berechnung von Taupunkt und Frostpunkt == | ||
Ausgangspunkt für die Berechnung des Taupunkts bzw. Frostpunkts sind die | Ausgangspunkt für die Berechnung des Taupunkts bzw. Frostpunkts sind die Magnus-Formeln für den Sättigungsdampfdruck über Wasser (1.1.) und Eis (1.2.).(siehe Einzelnachweise) | ||
:<math> | :<math> | ||
E_\mathrm{w} (\vartheta_\mathrm{d}) = E_0 \cdot \exp \left( \frac{17{,}5043 \cdot \vartheta_\mathrm{d}}{241{,}2\,^{\circ}\mathrm{C} + \vartheta_\mathrm{d}} \right) \qquad\qquad (1.1.) | E_\mathrm{w} (\vartheta_\mathrm{d}) = E_0 \cdot \exp \left( \frac{17{,}5043 \cdot \vartheta_\mathrm{d}}{241{,}2\,^{\circ}\mathrm{C} + \vartheta_\mathrm{d}} \right) \qquad\qquad (1.1.) | ||
| Zeile 111: | Zeile 110: | ||
== Einzelnachweise == | == Einzelnachweise == | ||
Dietrich Sonntag, Dirk Heinze: Sättigungsdampfdruck-und Sättigungsdampfdichtetafeln für Wasser und Eis. Deutscher Verlag für Grundstoffindustrie, Leipzig 1982 | |||
== Weblinks == | == Weblinks == | ||
| Zeile 117: | Zeile 116: | ||
* [http://www.top-wetter.de/calculator.htm Rechner für die wichtigsten meteorologischen Größen] | * [http://www.top-wetter.de/calculator.htm Rechner für die wichtigsten meteorologischen Größen] | ||
* [http://www.webgeo.de/beispiele/rahmen.php?string=1;k_202;1 WEBGEO-Modul: Kondensation und Feuchtemaße] WEBGEO - E-Learning-Portal für Geographie und Nachbarwissenschaften | * [http://www.webgeo.de/beispiele/rahmen.php?string=1;k_202;1 WEBGEO-Modul: Kondensation und Feuchtemaße] WEBGEO - E-Learning-Portal für Geographie und Nachbarwissenschaften | ||
[[category: PhysikGrundlagen]][[category: Review]] | |||
Aktuelle Version vom 17. Januar 2018, 10:21 Uhr
zurück zu Messgrößen
Diese Seite enthält bearbeitete Inhalte von http://de.wikipedia.org/wiki/Taupunkt (Version vom 08.03.2010: http://de.wikipedia.org/w/index.php?title=Taupunkt&oldid=70617916) Sie steht deshalb unter der Lizenz: „Creative Commons Attribution/Share Alike“
Als Taupunkt oder Taupunkttemperatur bezeichnet man die Temperatur, bei der sich auf einem Gegenstand (bei vorhandener Feuchte) ein Gleichgewichtszustand von kondensierendem und verdunstendem Wasser einstellt, mit anderen Worten die Kondensatbildung gerade einsetzt. Die fundamentale direkte Messung erfolgt mit einem Taupunktspiegelhygrometer, indirekte Messungen können z. B. auch mit Impedanz- oder mit Kapazitiven-Sensoren erfolgen.
Der Taupunkt einer Probe ist lediglich vom Druck abhängig, wohingegen die relative Feuchte eine von Druck und Temperatur abhängige Größe ist. Luft, die nicht vollständig mit Wasserdampf gesättigt ist, hat eine relative Feuchte kleiner als 100 % und kann – bei unveränderter Temperatur – weiteren Wasserdampf aufnehmen. Nimmt die Temperatur ab, nimmt auch die Aufnahmefähigkeit der Luft für Wasserdampf ab, das heißt, die relative Feuchte (rF) steigt an. Beim Taupunkt ist eine relative Feuchte von 100 % erreicht, es kommt also zur Kondensation. Dabei bildet sich auf festen oder flüssigen Grenzflächen ein Niederschlag, der Effekt ist stärker, je geringer die Temperatur der Grenzflächen ist, bzw. je höher die Luftfeuchte ist. Bekannte Beispiele sind das Beschlagen von kalten Brillengläsern, wenn man einen Raum mit feuchter Luft betritt und die Tröpfchenbildung an Getränkeflaschen, die gerade aus dem Kühlschrank genommen wurden. Die Taupunktkurve gibt bei gegebenem atmosphärischen Druck, für die jeweilige Temperatur, den Maximalwert von Feuchte an, die Luft (außerhalb der Übersättigung) aufnehmen kann (= 100 % rF Kurve).
Definition[Bearbeiten]
Der Taupunkt von Wasser im formalen Sinne ist der Kondensationspunkt reinen Wassers und damit ein Wertepaar aus Druck und Temperatur. Da sich diese jedoch an der Phasengrenzlinie eines Reinstoffes gegenseitig bedingen, hier im Speziellen der Kondensationskurve zwischen Tripelpunkt und kritischem Punkt, setzt man in der Regel den Temperaturwert des Taupunkts, also die Taupunkttemperatur, mit dem Taupunkt gleich. Es handelt sich dabei um diejenige Temperatur der feuchten Luft, bei der diese wasserdampfgesättigt wäre sowie bei abnehmender Temperatur kondensieren würde. In diesem Zustand würde die relative Luftfeuchte 100 % betragen und es herrschte der Sättigungsdampfdruck. Demnach hat diese bzw. dieser auch das Formelzeichen Td bei Angaben in K und td oder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vartheta_{\rm d}} bei Angaben in °C, wobei der Index d für das englische „dew point“ steht. Zusätzlich wird auch τ häufig als Formelzeichen gebraucht.
Bedeutung für die Meteorologie[Bearbeiten]
In der Meteorologie gibt der Taupunkt die Grenztemperatur an, bei der, in Abhängigkeit vom Luftdruck, der in der Luft enthaltene Wasserdampf gerade damit beginnt Kondensat (Tropfen, Eiskristalle) zu bilden.
Enthält beispielsweise 1 m³ Luft 50 g Wasserdampf, muss die Temperatur mindestens 40 °C betragen, damit sich keine Wassertröpfchen bilden. Bei Unterschreitung bilden sich bei Anwesenheit von Kondensationskeimen spontan Tröpfchen (Wolken).
Der Taupunkt und der Reifpunkt sind Zustände des Wassers in seinem Phasendiagramm, bei denen es zur Kondensation (zum Beispiel bei der Wolkenbildung) bzw. Resublimation (zum Beispiel als Reif) kommt.
Der Taupunkt als Maß für die Luftfeuchtigkeit ist eine abgeleitete, keine real vorliegende Temperatur und als solche normalerweise niedriger oder gleich der tatsächlichen Lufttemperatur. Sind beide gleich, so ist die Luft mit Wasserdampf gesättigt. Ein Feuchtemaß ist er deshalb, weil er abhängig vom Wasserdampfgehalt der Luft ist. Wird mit Wasserdampf gesättigte Luft unter den Taupunkt abgekühlt, so tritt Kondensation ein, welche sich in Beschlagen, Nebel, Tau bzw. allgemein in Niederschlag äußert. Einfach ausgedrückt: Je größer die Differenz zwischen Temperatur und Taupunkt ist, desto trockener ist die Luft. Wichtig für die Kondensation von Wasserpartikeln und die Vermeidung von größerer Übersättigung sind Aerosole als Kondensationskerne. Diese treten jedoch in der Regel überall in der Erdatmosphäre in ausreichender Anzahl auf, und verhindern dadurch größere Übersättigungen. Eine Besonderheit tritt während der Übersättigung ein, dann liegt die Taupunkttemperatur höher als die Lufttemperatur.
Taupunktdifferenz[Bearbeiten]
Die Taupunktdifferenz (engl. auch dew point spread genannt) ist ein weiteres Feuchtemaß und stellt die Differenz zwischen realer Luft- und Taupunkttemperatur dar. Je größer die Taupunktdifferenz, desto kleiner die relative Luftfeuchte und umgekehrt. Bei einer Differenz von Null, also identischer Luft- und Taupunkttemperatur, liegt Sättigung vor. In aufsteigender Luft verringert sich durch Temperaturabfall, den zeitgleichen Druckabfall überkompensierend, in zunehmender Höhe die Taupunktdifferenz, bis Sättigung erreicht ist.
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta \vartheta_{\rm d} = \vartheta - \vartheta_{\rm d} \!}
Das führt u. a. zu der uns bekannten Wolkenbildung am Himmel. Die Verringerung der Taupunktdifferenz bis hin zur Sättigung in bestimmten Arealen ist der Grund, warum die Wolken am Himmel an bestimmter Stelle sich in bestimmter Höhe quasi als „Schale“ um die Erde legen. Es sind Bereiche gleicher Sättigung.
Die Taupunktdifferenz beeinflusst auch das Wohlbefinden von Menschen, vor allem bei sommerlichen bzw. tropischen Temperaturen. So empfinden die meisten Menschen einen Taupunkt von 20 °C bei einer Lufttemperatur von 30 °C (Tropentag) als ein angenehmes Klima (ungefähr 55 % relative Luftfeuchtigkeit). Hingegen ist ein Taupunkt von 20 °C und eine Lufttemperatur von 22 °C (ungefähr 88 % relative Luftfeuchtigkeit) sehr unangenehm, man schwitzt und friert zugleich.
Frostpunkt[Bearbeiten]
Liegt ein Taupunkt bei Temperaturen unterhalb der Frostgrenze, sodass sich als Kondensat Eis bildet, wird ein solcher Taupunkt alternativ auch Frostpunkt, Eispunkt oder Reifpunkt genannt. Der Frostpunkt bezeichnet also Taupunkte an der Phasengrenze fest-gasförmig, welche im Bereich der Sublimation bzw. Resublimation liegen. Man bezeichnet daher auch die zugehörige Phasengrenzlinie, welche sich vom absoluten Nullpunkt bis zum Tripelpunkt erstreckt, als Sublimationskurve.
Das Formelzeichen des Frostpunktes ist Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_{\rm i}} oder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_{\rm f}} für Angaben in K und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_{\rm i}} bzw. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vartheta_{\rm i}} oder Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_{\rm f}} bzw. Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vartheta_{\rm f}} bei Angaben in °C.
Das ihm zurechenbare charakteristische Wetterphänomen, wiederum in Analogie zum Taupunkt, ist der Reif. Im Phasendiagramm des Wassers stellt der Frostpunkt den Temperaturwert der Sublimationskurve dar. Oft wird der Frostpunkt dem Taupunkt untergeordnet und dieser folglich als Sammelbegriff für beide Temperaturwerte verwendet.
Berechnung von Taupunkt und Frostpunkt[Bearbeiten]
Ausgangspunkt für die Berechnung des Taupunkts bzw. Frostpunkts sind die Magnus-Formeln für den Sättigungsdampfdruck über Wasser (1.1.) und Eis (1.2.).(siehe Einzelnachweise)
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_\mathrm{w} (\vartheta_\mathrm{d}) = E_0 \cdot \exp \left( \frac{17{,}5043 \cdot \vartheta_\mathrm{d}}{241{,}2\,^{\circ}\mathrm{C} + \vartheta_\mathrm{d}} \right) \qquad\qquad (1.1.) }
wobei gilt:
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -30~^{\circ}\mathrm{C} \leq \vartheta \leq 70~^{\circ}\mathrm{C} }
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_0 = E_\mathrm{w}\left(\vartheta = 0~^{\circ}\mathrm{C}\right) = 6{,}11213~\mathrm{hPa} }
und für den Frostpunkt
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_\mathrm{i} (\vartheta_\mathrm{f}) = E_0 \cdot \exp \left( \frac{22{,}4433 \cdot \vartheta_\mathrm{f}}{272{,}186\,^{\circ}\mathrm{C} + \vartheta_\mathrm{f}} \right) \qquad\qquad (1.2.) }
wobei gilt:
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle -60~^{\circ}\mathrm{C} \leq \vartheta \leq 0~^{\circ}\mathrm{C} }
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_0 (\vartheta = 0~^{\circ}\mathrm{C}) = 6{,}11153~\mathrm{hPa} }
Taupunkt in Abhängigkeit von Temperatur und Luftfeuchtigkeit. Sättigungsdampfdruck und Taupunkt/Frostpunkt sind Größen, die sich gegenseitig bedingen, sie sind also als Funktion voneinander direkt berechenbar, wie die obigen Gleichungen für den Fall E(t) zeigen. Dies resultiert daraus, dass die Dampfdruckkurve im Phasendiagramm mit den Ausnahmen von kritischem Punkt und Tripelpunkt genau einen Freiheitsgrad besitzt, was sich wiederum aus der Gibbsschen Phasenregel ableitet. Man kann daher die obigen Gleichungen umstellen und erhält so den Taupunkt in Abhängigkeit vom Sättigungsdampfdruck über Wasser (1.3.) und den Frostpunkt in Abhängigkeit vom Sättigungsdampfdruck über Eis (1.4.). Es gilt zu beachten, dass auch diese Gleichungen aufgrund ihrer Ungenauigkeit nur in den begrenzten Temperaturintervallen der Ausgangsgleichungen verwendet werden sollten. Diese Intervalle wurden entsprechend den Stoffdaten des Wassers auf dessen Werte umgerechnet. Beide Gleichungen ergeben Temperaturwerte in Grad Celsius und sind für einen Sättigungsdampfdruck in hPa ausgelegt.
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vartheta_\mathrm{d} (E_\mathrm{w}) = \frac{241{,}2 \cdot \left( \ln E_\mathrm{w} - \ln 6{,}11213 \right)}{17{,}5043 - \left( \ln E_\mathrm{w} - \ln 6{,}11213 \right)} \qquad\qquad (1.3.)}
wobei gilt:
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0{,}5106~\mathrm{hPa} \leq E_\mathrm{w} \leq 311{,}7731~\mathrm{hPa} }
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vartheta_{\rm f} (E_{\rm i})= \frac{272{,}186 \cdot \left( \ln E_{\rm i} - \ln 6{,}11153 \right)}{22{,}4433 - \left( \ln E_{\rm i} - \ln 6{,}11153 \right)} \qquad\qquad (1.4.)}
wobei gilt:
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0{,}010753~\mathrm{hPa} \leq E_\mathrm{i} \leq 6{,}11153~\mathrm{hPa} }
Diese Formeln sind jedoch unpraktisch, da meist nur die relative Luftfeuchtigkeit und die zugehörige Lufttemperatur zur Verfügung stehen. Über die Gleichung (2.1.) beziehungsweise (2.2.) lässt sich jedoch auch ein direkter Zusammenhang zwischen den Größen herstellen.
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi=\frac{E \left( \vartheta_{\rm d} \right) }{E \left( \vartheta \right) }\cdot 100\,% \qquad \qquad (2.1.) }
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E \left( \vartheta_{\rm d} \right) = \frac{\varphi \cdot E \left( \vartheta \right)}{100\,%} \qquad \qquad (2.2.) }
Nutzt man Gleichung (2.2.) und setzt in sie die Magnus-Formel (1.1.) ein, so erhält nach der Umstellung zum Taupunkt die Gleichung (2.3.), mit der sich dieser ausgehend von der relativen Luftfeuchtigkeit und der Lufttemperatur berechnen lässt. Setzt man stattdessen Gleichung (1.2.) in (2.2.) ein, so erhält man nach dem Umstellen die Gleichung (2.4.) zur Berechnung des Frostpunkts, ebenfalls in Abhängigkeit von der relativen Luftfeuchtigkeit und der Lufttemperatur.
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vartheta_{\rm d} \left( \varphi,\;\vartheta \right) = \frac{241{,}2 \cdot \ln \left( \frac{\varphi}{100\,} \right) + \frac{4222{,}03716 \cdot \vartheta}{241{,}2 + \vartheta}}{17{,}5043 - \ln \left( \frac{\varphi}{100\,} \right) - \frac{17{,}5043 \cdot \vartheta}{241{,}2 + \vartheta}} \qquad \qquad (2.3.)}
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vartheta_{\rm f} \left( \varphi,\;\vartheta \right) = \frac{272{,}186 \cdot \ln \left( \frac{\varphi}{100\,%} \right) + \frac{6107{,}85384 \cdot \vartheta}{272{,}186 + \vartheta}}{22{,}4433 - \ln \left( \frac{\varphi}{100\,%} \right) - \frac{22{,}4433 \cdot \vartheta}{272{,}186 + \vartheta}} \qquad \qquad (2.4.)}
Diese lassen sich bei Bedarf auch in Kelvin umrechnen:
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_{\rm d} = \frac{\left( \vartheta_{\rm d} + 273{,}15\,^{\circ}\mathrm{C}\right)\cdot \mathrm{K}}{1\,^{\circ}\mathrm{C}} }
- Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T_{\rm f} = \frac{\left( \vartheta_{\rm f} + 273{,}15\,^{\circ}\mathrm{C}\right)\cdot \mathrm{K}}{1\,^{\circ}\mathrm{C}} }
Einzelnachweise[Bearbeiten]
Dietrich Sonntag, Dirk Heinze: Sättigungsdampfdruck-und Sättigungsdampfdichtetafeln für Wasser und Eis. Deutscher Verlag für Grundstoffindustrie, Leipzig 1982
Weblinks[Bearbeiten]
- Vaisala Feuchterechner Rechnet Größen wie Relative Feuchte, Taupunkt, Konzentration (ppm), Absolute Feuchte, […] ineinander um. Als Flash und Windows-Programm verfügbar.
- Rechner für die wichtigsten meteorologischen Größen
- WEBGEO-Modul: Kondensation und Feuchtemaße WEBGEO - E-Learning-Portal für Geographie und Nachbarwissenschaften