Doppelbrechung: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Autoren: [[Benutzer:Hschwarz|Hans-Jürgen Schwarz]], [[Benutzer:AHusen|Anika Husen]] | Autoren: [[Benutzer:Hschwarz|Hans-Jürgen Schwarz]], [[Benutzer:AHusen|Anika Husen]] | ||
| Zeile 6: | Zeile 5: | ||
== Zusammenfassung == | == Zusammenfassung == | ||
Die Doppelbrechung ist ein Phänomen, bei dem ein | Die Doppelbrechung ist ein Phänomen, bei dem ein Lichtstrahl in zwei Strahlen aufgespalten wird, wenn er die Grenzfläche eines optisch anisotropen Körpers passiert. Dabei entstehen zwei Strahlen mit unterschiedlicher Lichtgeschwindigkeit je nach der Ausbreitungsrichtung innerhalb des Körpers. Einer dieser Strahlen wird normal gebrochen (ordentlicher Strahl) und einer erfährt eine Richtungsänderung, der außerordentliche Strahl. Der [[Gangunterschied]], der zwischen den beiden unterschiedlich schnellen Strahlenbündeln entsteht, führt zu den Interferenzfarbe. Die überwiegende Zahl der Salze sind optisch anisotrop, d.h. dort erfährt ein Lichtstrahl die Doppelbrechung. Nur Materialien, deren innerer Aufbau dem kubischen Kristallsystem zugerechnet werden kann, sind optisch isotrop. | ||
<br> | <br> | ||
<!-- | |||
== Einleitung == | == Einleitung == | ||
--> | |||
<br> | <br> | ||
== Anisotrope Körper == | == Anisotrope Körper == | ||
Salze bilden Kristalle mit verschiedenen [[Kristallsystem|Kristallsystemen]] aus, deren Atome in einer Gitterstuktur angeordnet sind. Bestimmte Gitteraufbauten besitzen jeweils verschiedene optische Eigenschaften. Diese äußern sich u.a. in der Fortpflanzungsgeschwindigkeit von Lichtwellen beim Durchstrahlen des Gitters. Bei optisch anisotropen Körpern ist diese abhängig von der Richtung der Strahlung innerhalb des Gitters. == Brechungsindex-Doppelbrechung == Zur Beschreibung der Durchlassgeschwindigkeit wird der Begriff der optische Dichte verwendet, wobei Körper mit einer höheren optischen Dichte eine geringere Lichtgeschwindigkeit aufweisen. Der Wert der Lichtbrechung/Brechungsindex beschreibt das Verhältnis der Lichtgeschwindigkeit im Vakuum und der | Salze bilden Kristalle mit verschiedenen [[Kristallsystem|Kristallsystemen]] aus, deren Atome in einer Gitterstuktur angeordnet sind. Bestimmte Gitteraufbauten besitzen jeweils verschiedene optische Eigenschaften. Diese äußern sich u.a. in der Fortpflanzungsgeschwindigkeit von Lichtwellen beim Durchstrahlen des Gitters. Bei optisch anisotropen Körpern ist diese abhängig von der Richtung der Strahlung innerhalb des Gitters <ref>http://www.olympusmicro.com/primer/lightandcolor/birefringence.html</ref>. | ||
Im Falle anisotroper Kristalle wird das Licht nicht nur gebrochen, sondern auch in zwei Transversalwellen aufgespalten, die sich durch verschiedene Geschwindigkeit und damit unterschiedliche Lichtbrechung auszeichnen. Dieses Phänomen wird Doppelbrechung (Delta) genannt. | |||
Treten Lichtwellen in ein anisotropes Medium ein, so erfolgt nicht nur eine Doppelbrechung, sondern auch Polarisation: Die beiden Transversalwellen werden in ihrer Schwingungsform dergestalt verändert, dass sie jeweils aufeinander senkrecht stehend nur noch in einer Richtung schwingen. Sie sind damit linear polarisiert. | |||
Betrachtet man ein Modell, in dem, beginnend vom Mittelpunkt, alle Lichtgeschwindigkeiten eines Minerals in alle Raumrichtungen aufgetragen sind, so bildet die einhüllende Raumschale für diejenigen Minerale eine Kugel, die dem kubischen Kristallsystem angehören. Man nennt dieses Modell eine Indikatrix. | |||
Die Indikatrix der hexagonalen, trigonalen und der tetragonalen Kristallsyteme (wirtelige Systeme) stellt einen zweiachsigen Ellipsoid dar, einen Rotationsellipsoiden. Diese Minerale werden als optisch einachsig bezeichnet. Die Indikatrix der anderen Kristallsysteme (rhombisch, monoklin, triklin) ist ein dreiachsiger Ellipsoid mit zwei optischen Achsen der Isotropie. | |||
== Brechungsindex-Doppelbrechung == | |||
Zur Beschreibung der Durchlassgeschwindigkeit wird der Begriff der optische Dichte verwendet, wobei Körper mit einer höheren optischen Dichte eine geringere Lichtgeschwindigkeit aufweisen. Der Wert der Lichtbrechung/Brechungsindex beschreibt das Verhältnis der Lichtgeschwindigkeit im Vakuum und der Lichtgeschwindigkeit innerhalb des betrachteten Körpers. Die Lichtgeschwindigkeit im Vakuum ist die schnellste, somit sind alle Brechungsindizes anderer Materialien kleiner als 1. Die Differenz des höchsten und niedrigsten Brechungsindex eines Kristalls wird als Doppelbrechung bezeichnet. <br> | |||
| Zeile 23: | Zeile 31: | ||
| bgcolor="yellow" align="center"| <math>n_x = \frac{c_{Licht}}{c_x}</math> | | bgcolor="yellow" align="center"| <math>n_x = \frac{c_{Licht}}{c_x}</math> | ||
|- | |- | ||
| bgcolor="yellow" | n<sub>x</sub> = | | bgcolor="yellow" | n<sub>x</sub> = Lichtbrechung, C<sub>Licht</sub> = Lichtgeschwindigkeit im Vakuum, c<sub>x</sub> = Lichtgeschwindigkeit im Material X | ||
|} | |} | ||
[[Datei:Mueller-Indikatrix1.jpg|thumb|350px|left|'''A: Strahlengeschwindigkeitsfläche''' Für jede Strahlrichtung wird vom Mittelpunkt aus der Wert der Geschwindigkeit abgetragen. Die resultierende Hüllform ist eine Kugel mit dem Radius v. ' '''B: Indikatrix''' Für jede Strahlrichtung wird parallel zur Schwingungsrichtung und senkrecht zum Strahl der Wert der Lichtbrechung abgetragen. Die resultierende Hüllform ist eine Kugel mit dem Radius n. In jeder Strahlrichtung sind unendlich viele Schwingungsrichtungen möglich. <bib id="Raith.etal:2009"></bib>]] | |||
Bei optisch anisotropen (nicht kubischen) Kristallen findet eine Doppelbrechung statt. Diese unterscheidet sich von der einfachen Lichtbrechung, die an jeder Grenzfläche zwischen optisch unterschiedlich dichten Medien eine Ablenkung der Strahlungsrichtung und eine Aufspaltung der Spektralfarben bewirkt, und steht im Zusammenhang mit einer Änderung der Wellenlänge und einer von dieser abhängigen Richtungsänderung. Bei der Doppelbrechung wird das polarisierte Licht an der Grenzfläche des Kristalls in zwei Strahlengänge aufgespalten, die entlang aufeinander senkrecht stehender Durchlassebenen umpolarisiert sind. Es entstehen der ordentliche und der außerordentliche Strahl. Der ordentliche Strahl wird mit einem konstanten Brechungsindex (n<sub>o</sub>) gebrochen. Der außerordentliche Strahl hat seine Polarisationsrichtung senkrecht zu der des ordentlichen Strahles und einen Brechungsindex (n<sub>e</sub>), der von seiner Richtung innerhalb des Kristalls abhängt. Die graphische Darstellung der unterschiedlichen Brechungsindizes in alle Raumrichtungen bildet die so genannte Indikatrix. | Bei optisch anisotropen (nicht kubischen) Kristallen findet eine Doppelbrechung statt. Diese unterscheidet sich von der einfachen Lichtbrechung, die an jeder Grenzfläche zwischen optisch unterschiedlich dichten Medien eine Ablenkung der Strahlungsrichtung und eine Aufspaltung der Spektralfarben bewirkt, und steht im Zusammenhang mit einer Änderung der Wellenlänge und einer von dieser abhängigen Richtungsänderung. Bei der Doppelbrechung wird das polarisierte Licht an der Grenzfläche des Kristalls in zwei Strahlengänge aufgespalten, die entlang aufeinander senkrecht stehender Durchlassebenen umpolarisiert sind. Es entstehen der ordentliche und der außerordentliche Strahl. Der ordentliche Strahl wird mit einem konstanten Brechungsindex (n<sub>o</sub>) gebrochen. Der außerordentliche Strahl hat seine Polarisationsrichtung senkrecht zu der des ordentlichen Strahles und einen Brechungsindex (n<sub>e</sub>), der von seiner Richtung innerhalb des Kristalls abhängt. Die graphische Darstellung der unterschiedlichen Brechungsindizes in alle Raumrichtungen bildet die so genannte Indikatrix. | ||
[[Datei:Mueller-Indikatrix2.jpg|thumb|350px|left| aus <bib id="Raith.etal:2009"></bib>]] Dafür werden die Brechungsindizes von einem Punkt aus in alle Raumrichtung als Vektoren dargestellt, deren Länge dem jeweiligen Brechungsindex entspricht. Bei optisch einachsigen Kriatallen bildet sie einen Rotationsellipsoid mit der optischen Achse als Achse des Ellipsoids. Die Indikatrix optisch zweiachsiger Kristalle bildet ein kompliziertes Doppelschalenmodell, kubische Systeme erhalten eine Kugel. | [[Datei:Mueller-Indikatrix2.jpg|thumb|350px|left| aus <bib id="Raith.etal:2009"></bib>]] Dafür werden die Brechungsindizes von einem Punkt aus in alle Raumrichtung als Vektoren dargestellt, deren Länge dem jeweiligen Brechungsindex entspricht. Bei optisch einachsigen Kriatallen bildet sie einen Rotationsellipsoid mit der optischen Achse als Achse des Ellipsoids. Die Indikatrix optisch zweiachsiger Kristalle bildet ein kompliziertes Doppelschalenmodell, kubische Systeme erhalten eine Kugel. | ||
| Zeile 55: | Zeile 58: | ||
== Interferenzfarben == | == Interferenzfarben == | ||
Zur Identifizierung einer Phase kann die Betrachtung der Interferenzfarben hilfreich sein. Diese werden bei gekreuzten Polarisatoren sichtbar und entstehen durch den Gangunterschied, der durch die Doppelbrechung erzeugt wird. Je nach Größe des Gangunterschiedes erscheint der Kristall im Dunkelfeld in einer bestimmten Farbe. Die farbliche Erscheinung steht im Zusammenhang mit der Wellenlänge, die durch den Gangunterschied des doppelt gebrochenen Lichtes positive Interferenz erfährt. Somit ist die Farbe genau wie der Gangunterschied selbst sowohl von den Brechungsindizes als auch von der Dicke des Kristalles abhängig. Ist die ungefähre Dicke des Kristalles bekannt, können die Brechungsindizes unter Betrachtung der Interferenzfarben abgeschätzt werden. Dabei wird stets die Hellstellung also die maximale Doppelbrechung betrachtet. Dazu empfiehlt es sich eine Farbtafel nach Michel-Lévy <ref>http://www.zeiss.com/C1256CFB00332E16/0/FECC5775A0897BCCC1256D08002A4E39/$file/46-0014_d.pdf gelesen 28.07.2010 </ref> zur Hilfe zu nehmen. Diese zeigt den Zusammenahng zwischen den Interferenzfarben bzw. des Gangunterschiedes und den Brechungsindizes in Abhängigkeit von der Dicke des durchstrahlten Objektes. | Zur Identifizierung einer Phase kann die Betrachtung der Interferenzfarben hilfreich sein. Diese werden bei gekreuzten Polarisatoren sichtbar und entstehen durch den [[Gangunterschied]], der durch die Doppelbrechung erzeugt wird. Je nach Größe des Gangunterschiedes erscheint der Kristall im Dunkelfeld in einer bestimmten Farbe. Die farbliche Erscheinung steht im Zusammenhang mit der Wellenlänge, die durch den Gangunterschied des doppelt gebrochenen Lichtes positive Interferenz erfährt. Somit ist die Farbe genau wie der Gangunterschied selbst sowohl von den Brechungsindizes als auch von der Dicke des Kristalles abhängig. Ist die ungefähre Dicke des Kristalles bekannt, können die Brechungsindizes unter Betrachtung der Interferenzfarben abgeschätzt werden. Dabei wird stets die Hellstellung also die maximale Doppelbrechung betrachtet. Dazu empfiehlt es sich eine Farbtafel nach Michel-Lévy <ref>http://www.zeiss.com/C1256CFB00332E16/0/FECC5775A0897BCCC1256D08002A4E39/$file/46-0014_d.pdf gelesen 28.07.2010 </ref> zur Hilfe zu nehmen. Diese zeigt den Zusammenahng zwischen den Interferenzfarben bzw. des Gangunterschiedes und den Brechungsindizes in Abhängigkeit von der Dicke des durchstrahlten Objektes. | ||
== Weblinks == | == Weblinks == | ||
| Zeile 65: | Zeile 67: | ||
== Literatur == | == Literatur == | ||
< | <biblist/> | ||
[[Category:LichtMikroskopie]] [[Category: | [[Category:LichtMikroskopie]] [[Category:Husen,Anika]] [[Category:Review]] [[Category:R-MSteiger]] [[Category:R-CBlaeuer]] | ||
Aktuelle Version vom 16. Juli 2012, 20:43 Uhr
Autoren: Hans-Jürgen Schwarz, Anika Husen
zurück zu Polarisationsmikroskopie
Zusammenfassung[Bearbeiten]
Die Doppelbrechung ist ein Phänomen, bei dem ein Lichtstrahl in zwei Strahlen aufgespalten wird, wenn er die Grenzfläche eines optisch anisotropen Körpers passiert. Dabei entstehen zwei Strahlen mit unterschiedlicher Lichtgeschwindigkeit je nach der Ausbreitungsrichtung innerhalb des Körpers. Einer dieser Strahlen wird normal gebrochen (ordentlicher Strahl) und einer erfährt eine Richtungsänderung, der außerordentliche Strahl. Der Gangunterschied, der zwischen den beiden unterschiedlich schnellen Strahlenbündeln entsteht, führt zu den Interferenzfarbe. Die überwiegende Zahl der Salze sind optisch anisotrop, d.h. dort erfährt ein Lichtstrahl die Doppelbrechung. Nur Materialien, deren innerer Aufbau dem kubischen Kristallsystem zugerechnet werden kann, sind optisch isotrop.
Anisotrope Körper[Bearbeiten]
Salze bilden Kristalle mit verschiedenen Kristallsystemen aus, deren Atome in einer Gitterstuktur angeordnet sind. Bestimmte Gitteraufbauten besitzen jeweils verschiedene optische Eigenschaften. Diese äußern sich u.a. in der Fortpflanzungsgeschwindigkeit von Lichtwellen beim Durchstrahlen des Gitters. Bei optisch anisotropen Körpern ist diese abhängig von der Richtung der Strahlung innerhalb des Gitters [1].
Im Falle anisotroper Kristalle wird das Licht nicht nur gebrochen, sondern auch in zwei Transversalwellen aufgespalten, die sich durch verschiedene Geschwindigkeit und damit unterschiedliche Lichtbrechung auszeichnen. Dieses Phänomen wird Doppelbrechung (Delta) genannt. Treten Lichtwellen in ein anisotropes Medium ein, so erfolgt nicht nur eine Doppelbrechung, sondern auch Polarisation: Die beiden Transversalwellen werden in ihrer Schwingungsform dergestalt verändert, dass sie jeweils aufeinander senkrecht stehend nur noch in einer Richtung schwingen. Sie sind damit linear polarisiert. Betrachtet man ein Modell, in dem, beginnend vom Mittelpunkt, alle Lichtgeschwindigkeiten eines Minerals in alle Raumrichtungen aufgetragen sind, so bildet die einhüllende Raumschale für diejenigen Minerale eine Kugel, die dem kubischen Kristallsystem angehören. Man nennt dieses Modell eine Indikatrix. Die Indikatrix der hexagonalen, trigonalen und der tetragonalen Kristallsyteme (wirtelige Systeme) stellt einen zweiachsigen Ellipsoid dar, einen Rotationsellipsoiden. Diese Minerale werden als optisch einachsig bezeichnet. Die Indikatrix der anderen Kristallsysteme (rhombisch, monoklin, triklin) ist ein dreiachsiger Ellipsoid mit zwei optischen Achsen der Isotropie.
Brechungsindex-Doppelbrechung[Bearbeiten]
Zur Beschreibung der Durchlassgeschwindigkeit wird der Begriff der optische Dichte verwendet, wobei Körper mit einer höheren optischen Dichte eine geringere Lichtgeschwindigkeit aufweisen. Der Wert der Lichtbrechung/Brechungsindex beschreibt das Verhältnis der Lichtgeschwindigkeit im Vakuum und der Lichtgeschwindigkeit innerhalb des betrachteten Körpers. Die Lichtgeschwindigkeit im Vakuum ist die schnellste, somit sind alle Brechungsindizes anderer Materialien kleiner als 1. Die Differenz des höchsten und niedrigsten Brechungsindex eines Kristalls wird als Doppelbrechung bezeichnet.
| Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_x = \frac{c_{Licht}}{c_x}} |
| nx = Lichtbrechung, CLicht = Lichtgeschwindigkeit im Vakuum, cx = Lichtgeschwindigkeit im Material X |
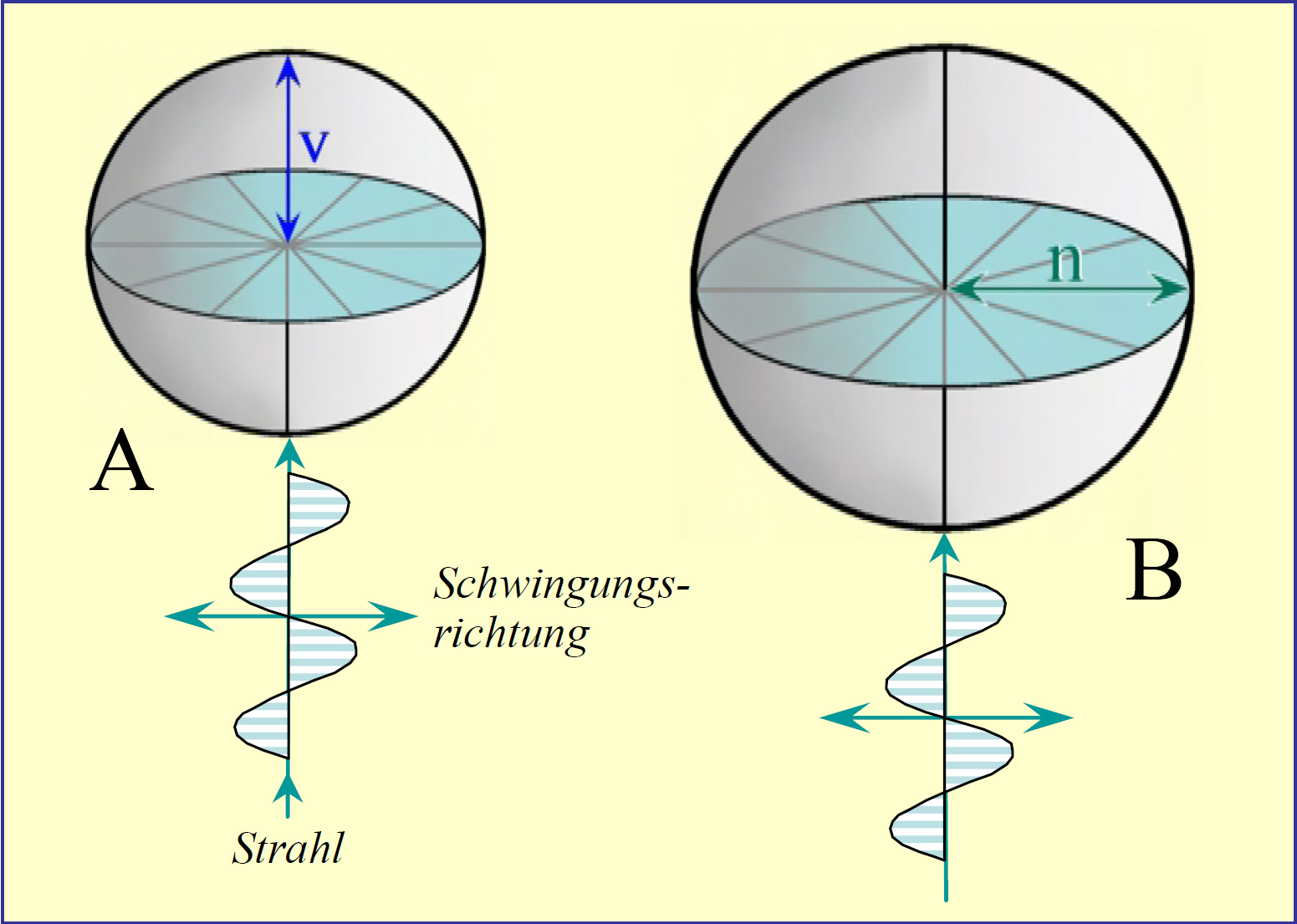
Autor / Verfasser: Raith, Michael M.; Raase, Peter

Bei optisch anisotropen (nicht kubischen) Kristallen findet eine Doppelbrechung statt. Diese unterscheidet sich von der einfachen Lichtbrechung, die an jeder Grenzfläche zwischen optisch unterschiedlich dichten Medien eine Ablenkung der Strahlungsrichtung und eine Aufspaltung der Spektralfarben bewirkt, und steht im Zusammenhang mit einer Änderung der Wellenlänge und einer von dieser abhängigen Richtungsänderung. Bei der Doppelbrechung wird das polarisierte Licht an der Grenzfläche des Kristalls in zwei Strahlengänge aufgespalten, die entlang aufeinander senkrecht stehender Durchlassebenen umpolarisiert sind. Es entstehen der ordentliche und der außerordentliche Strahl. Der ordentliche Strahl wird mit einem konstanten Brechungsindex (no) gebrochen. Der außerordentliche Strahl hat seine Polarisationsrichtung senkrecht zu der des ordentlichen Strahles und einen Brechungsindex (ne), der von seiner Richtung innerhalb des Kristalls abhängt. Die graphische Darstellung der unterschiedlichen Brechungsindizes in alle Raumrichtungen bildet die so genannte Indikatrix.
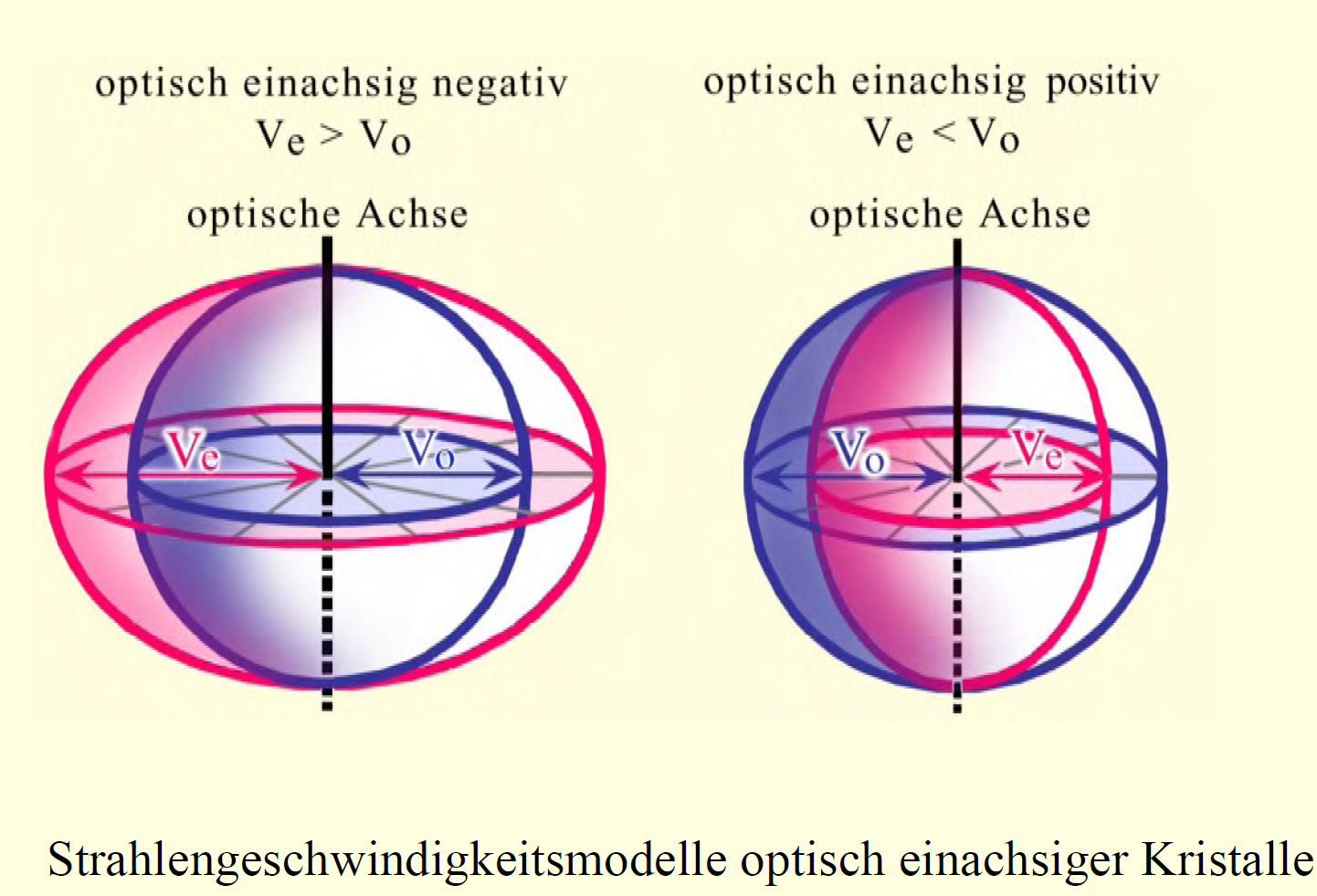
Autor / Verfasser: Raith, Michael M.; Raase, Peter

Dafür werden die Brechungsindizes von einem Punkt aus in alle Raumrichtung als Vektoren dargestellt, deren Länge dem jeweiligen Brechungsindex entspricht. Bei optisch einachsigen Kriatallen bildet sie einen Rotationsellipsoid mit der optischen Achse als Achse des Ellipsoids. Die Indikatrix optisch zweiachsiger Kristalle bildet ein kompliziertes Doppelschalenmodell, kubische Systeme erhalten eine Kugel.
Ordentlicher - außerordentlicher Strahl[Bearbeiten]
Zwischen den beiden unterschiedlich schnellen Strahlenbündeln entsteht ein Gangunterschied. Dieser führt für die Wellenlänge zu positiver Interferenz, deren ganzzahliges Vielfaches dieser Gangunterschied bildet. Somit erscheint der Kristall in einer bestimmten Farbe, die als Interferenzfarbe beschrieben wird.
Auslöschung[Bearbeiten]
Je nach der Ausrichtung der Durchlassebenen des Kristalles kann sich dieser in der Normal-/Dunkelstellung oder in der Hellstellung befinden. Die Normalstellung wiederholt sich vier mal alle 90° beim Drehen des Kristalls auf dem Objekttisch. In dieser sind die Durchlassrichtungen des Kristalls mit denen der Polarisatoren des Mikroskops deckungsgleich. Dies hat zur Folge, dass das Licht nicht durch den Kristall umpolarisiert wird, weil die Strahlung beim Auftreffen auf den Kristall bereits in einer Durchlassebene schwingt. So entsteht kein außerordentlicher Strahl und das Licht trifft mit einer einfachen Polarisation auf den Analysator, die senkrecht zu dessen Durchlassebene ist. Dadurch kann das Licht, das den Kriatall auf diese Weise durchstrahlt hat, den Analysator nicht durchstrahlen und trägt auch nicht zu dem wahrgenommenen Bild bei. Dieses Phänomen wird als Auslöschung bezeichnet.
Befindet sich der Kristall in einer Ausrichtung, in der keine seiner Durchlassebenen parallel zu der des Polarisators stehen, findet die Doppelbrechung statt. Das elliptisch polarisierte Licht, das auf den Analysator trifft, wird durch diesen wieder in eine Schwingungsebene gelenkt, so dass der Kristall sichtbar erscheint. Dessen Farbe ist abhängig von dem durch den Kristall erzeugten Gangunterschied, der wiederum von der Differenz der Brechungsindizes in den durchstrahlten Richtungen, also dem Wert der Doppelbrechung, bestimmt ist. Die Intensität des Gangunterschiedes wird außerdem von der Länge der durchstrahlten Strecke, also der Dicke des Kristalls beeinflusst.
Die Orientierung der Dunkelstellung ist von den Kristallgittereigenschaften abhängig und lässt deshalb Schlüsse auf das betrachtete Kristallsystem zu. Zeigt der Kristall in Normalstellung eine parlallele oder senkrechte Ausrichtung zur Horizontallinie, was an der Orientierung von Spaltflächen oder des Habitus erkennbar ist, so wird er als symmetrisch oder parallel auslöschend bezeichnet. Ist die Orientierung in Normalstellung weder parallel noch senkrecht zur Horizontallinie, nennt man das Auslöschungsverhalten schief. Die Abschätzung des Winkels der Auslöschungsstellung kann bei der genauen Identifizierung eines Minerales helfen.
Interferenzfarben[Bearbeiten]
Zur Identifizierung einer Phase kann die Betrachtung der Interferenzfarben hilfreich sein. Diese werden bei gekreuzten Polarisatoren sichtbar und entstehen durch den Gangunterschied, der durch die Doppelbrechung erzeugt wird. Je nach Größe des Gangunterschiedes erscheint der Kristall im Dunkelfeld in einer bestimmten Farbe. Die farbliche Erscheinung steht im Zusammenhang mit der Wellenlänge, die durch den Gangunterschied des doppelt gebrochenen Lichtes positive Interferenz erfährt. Somit ist die Farbe genau wie der Gangunterschied selbst sowohl von den Brechungsindizes als auch von der Dicke des Kristalles abhängig. Ist die ungefähre Dicke des Kristalles bekannt, können die Brechungsindizes unter Betrachtung der Interferenzfarben abgeschätzt werden. Dabei wird stets die Hellstellung also die maximale Doppelbrechung betrachtet. Dazu empfiehlt es sich eine Farbtafel nach Michel-Lévy [2] zur Hilfe zu nehmen. Diese zeigt den Zusammenahng zwischen den Interferenzfarben bzw. des Gangunterschiedes und den Brechungsindizes in Abhängigkeit von der Dicke des durchstrahlten Objektes.
Weblinks[Bearbeiten]
Literatur[Bearbeiten]
| [Raith.etal:2009] | Raith, Michael M.; Raase, Peter (2009): Leitfaden zur Dünnschliffmikroskopie, online Publikation |   |